Pythonを勉強するために本を買ったけど,積読してる.
最初の方の数値や算術演算,文字列の扱いで止まっている.
リストやタプル,辞書と似ているけど違いは何?
できる操作は違うの?
そんな方が,集合を理解して,比較演算や論理演算の学習に進むための記事です.
本記事の内容
複合データ型について,「リスト」,「タプル」,「辞書」に続き,今回は「集合」です.まずは集合の作成とデータ(個々の要素)の確認,変換を,その後要素の変更方法などを解説します.これまでの記事と同様に,コードを打ちながら学んで行きましょう.余力のある方は,部分的にコードを変更して実験してみましょう.
集合とは|作成方法
集合を扱うデータ型です.表1に示すように,辞書と同様にミュータブルに○,シーケンスに×をつけています.要素の順序が管理されていないので,オフセットを使いません.言い換えると,辞書からvalueを除き,keyだけにしたオブジェクトです.
表1.複合データ型
| 型(クラス) | ミュータブル | シーケンス型 |
|---|---|---|
| リスト(lis | ○ | ○ |
| タプル(tuple) | × | ○ |
| 辞書(dict) | ○ | × |
| 集合(set) | ○ | × |
高校数学で「集合」を学習しましたよね...そのイメージと同じように,個々の要素があるかどうかだけが分かれば良い場合に使用されます.まずは,集合の作成方法を学びながら,実行結果がどのように表示されるかをみてみましょう.同時に,入力ルールの理解を深めましょう.
集合の作成
要素をカンマで区切って並べ,{}(波括弧)で囲んで記述します.リストやタプルと同様に,変数に代入して,長いデータを短いコードで表現できます.辞書のkeyと同様に,文字列・数値・タプルなどの変更不可のデータを指定できますが,リスト・辞書などの変更可能なデータを指定できません.
1つ以上の要素をカンマで区切り,{}(波括弧)で囲んで記述する.
{-3, -2, -1, 0, 1, 2, 3}
{"さ", "し", "す", "せ", "そ"}
set()関数を用いて作成する.
set((-3, -2, -1, 0, 1, 2, 3)) # set()関数の引数も()で囲む.
set(("さ", "し", "す", "せ", "そ"))
変数に集合を代入できる.
set_ex1={-3, -2, -1, 0, 1, 2, 3}
set_ex1
set_ex2 = {"さ", "し", "す", "せ", "そ"}
set_ex2
異なる型が混在しても良い.
set_ex3 = {"hundred", 1000, 1E6, 1E9, 0+1j}
set_ex3
set_ex4_1 = {"さ", (“砂糖", "酒", "みりん”), "し", "す", "せ", "そ"}
set_ex4_1 # 文字列・数値・タプルなどの変更不可のデータを指定できる.
ただし,リスト・辞書などの変更可能なデータを指定できません.
set_ex4_2 = {"さ", {"砂糖", "酒", "みりん"}, "し", "す", "せ", "そ"}
set_ex4_2
TypeError Traceback (most recent call last)
—-> 1 set_ex4_2 = {“さ”, {“砂糖”, “酒”, “みりん”}, “し”, “す”, “せ”, “そ”}
2 set_ex4_2
TypeError: unhashable type: ‘set’
要素は重複しない.
set_ex5 = {"さ", "さ", "さ", "し", "し", "し", "す", "す", "す", "せ", "せ", "せ", "そ"}
set_ex5
何も記述しない場合,空集合となる.
set_empty=set() # 空集合はset()関数を使って記述する. set_empty
Pythonでは先に辞書が含まれたため,{}を入力すると,空辞書が作成されます.そのため,出力が{}ではなく,set()となっています.
まとめ
- 1つ以上の要素をカンマで区切り,{}(波括弧)で囲んで記述する.
- set()関数を用いて作成できる.
- 変数に集合を代入できる.
- 異なる型が混在しても良い.
- keyは重複しない.
- 何も記述しない場合,空集合となる.
集合のデータ型の確認
type()関数を使って確認します.「set」と表示されるか確認してみましょう.
type(set_ex3)
集合へのデータ型の変換
文字列,リスト,タプル,辞書は,集合と同じシーケンスでしたね.重複する値を除けば,オブジェクトをお互いに変換することができます.
文字列を集合に変換
set("集合にするで!”)
リストを集合に変換
set(['集', '合', 'に', 'す', 'る', 'で', '!'])
タプルを集合に変換
set(('集', '合', 'に', 'す', 'る', 'で', '!'))
辞書から集合に変換
set()関数に辞書を渡すと,keyが集合として返ってきます.
set({"さ":"砂糖", "し":"塩", "す":"酢", "せ":"醤油", "そ":"味噌"})
集合の操作
| 操作 | 関数・メソッド | 演算子ほか |
|---|---|---|
| 連結 | .update() | |
| 追加 | .add() | |
| 削除 | .clear(), .discard(), .pop(), .remove() | |
| 検索 | len() | in |
要素の連結
.update()メソッド → 別の集合を連結する.
prime1 = {2, 3, 5, 7, 11}
prime2 = {13, 17, 19, 23}
prime1.update(prime2) # prime1の末尾に,prime2が連結する.
prime1
要素の追加
.add()メソッド → 集合に要素を追加する.
prime1 = {2, 3, 5, 7, 11}
prime1.add(13) # prime1の末尾に,prime2が連結する.
prime1
要素の削除
.clear()メソッド → 全ての要素を削除する.
unneed = {"hard working", "deadline", "tax"}
unneed.clear()
unneed
.discard()メソッド → 要素の値を指定して削除する.
life = {"family", "health", "hobby", "money", "work"}
life.discard("work")
life
.pop()メソッド → 集合の中のいずれか1つの要素を削除する.
unneed = {"hard working", "deadline", "tax"}
unneed.pop()
unneed
リストでは引数にオフセットをしてできましたが,集合では順序がないので,どの要素を削除するかは指定できません.
私のコンピュータでは,”hard working”が削除されました...
.remove()メソッド → 要素の値を指定して削除する.
life = {"family", "health", "hobby", "money", "work"}
life.remove("work")
life
要素の検索
len()関数
len(life)
in → 要素の有無を調べる.
Trueと返ってきたら,要素が有り,Falseと返ってきたら要素は無いという判定です.TrueとFalse(論理値)のことを詳しく説明していないので,ここでは有無(真偽)をこのように確認するんだなくらいの理解で結構です.
"family" in life
"work" in life
集合演算

集合演算は,複数の集合についてある要素の有無などを確認できる演算子です.和集合・積集合・差集合・対称差がサポートされています.同様の操作を行えるメソッドも用意されています.
表3.集合演算子とメソッド
| 演算 | 集合演算子 | メソッド |
|---|---|---|
| 和集合 | | | .union() |
| 差集合 | -(マイナス記号ではなくハイフン) | .difference() |
| 積集合 | & | .intersection() |
| 対称差(排他的論理和) | ^ | .symetric_difference() |
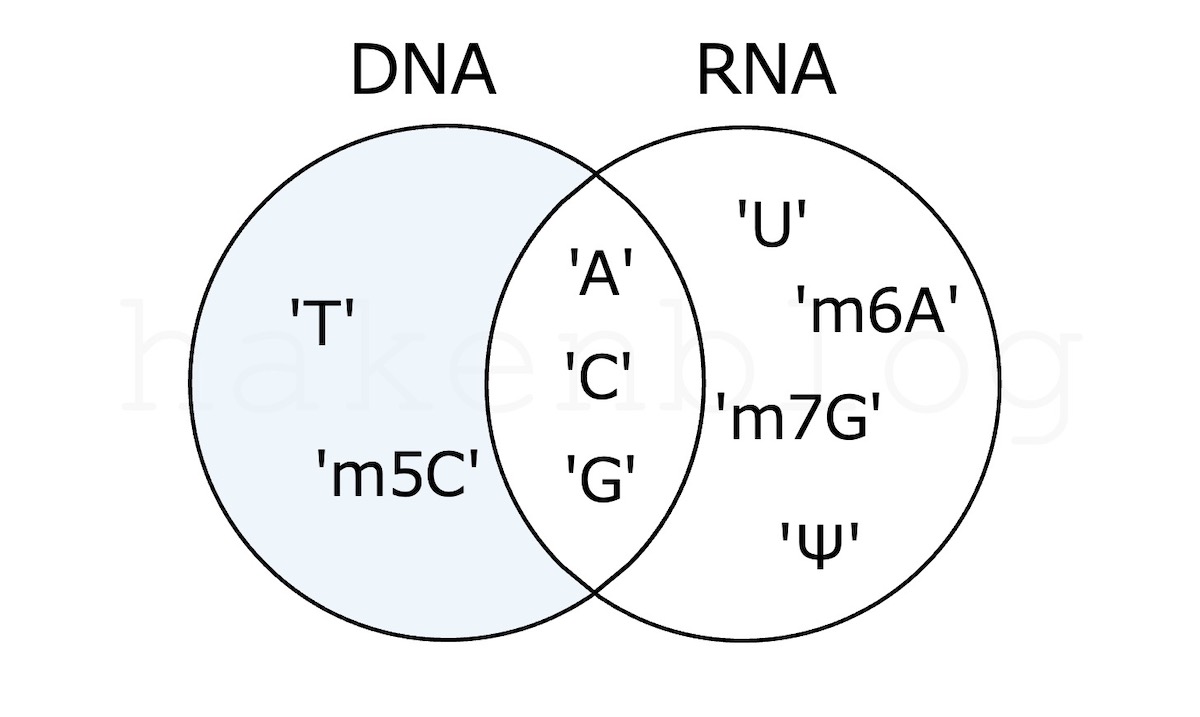
「DNA」,「RNA」という変数に保存された塩基,修飾塩基の集合を例に,練習してみましょう.
DNA = {"A", "T", "C", "m5C", "G"}
RNA = {"A", "m6A", "U", "Ψ", "C", "G", "m7G"}
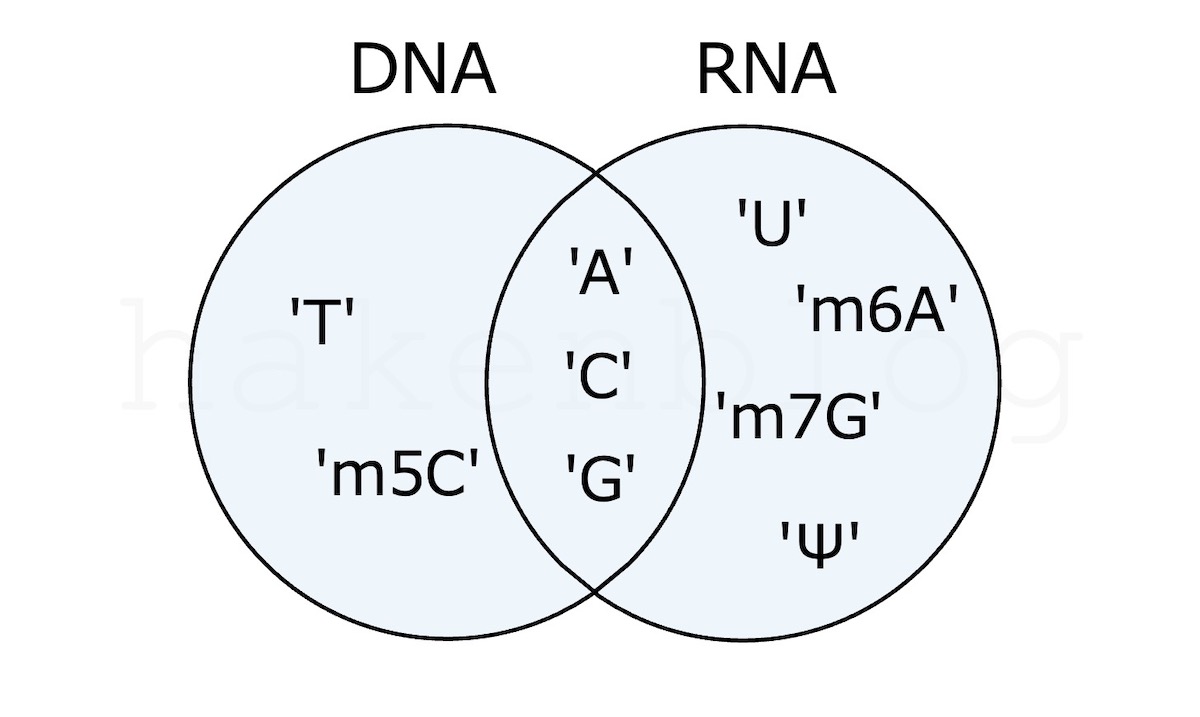
和集合
DNA | RNA
DNA.union(RNA)
差集合
集合Aに含まれていて,集合Bには含まれていない要素の集合を得ます.
ここでは,DNAに含まれていてRNAに含まれていない要素,またはその逆を出力しています.
DNA - RNA
DNA.difference(RNA)
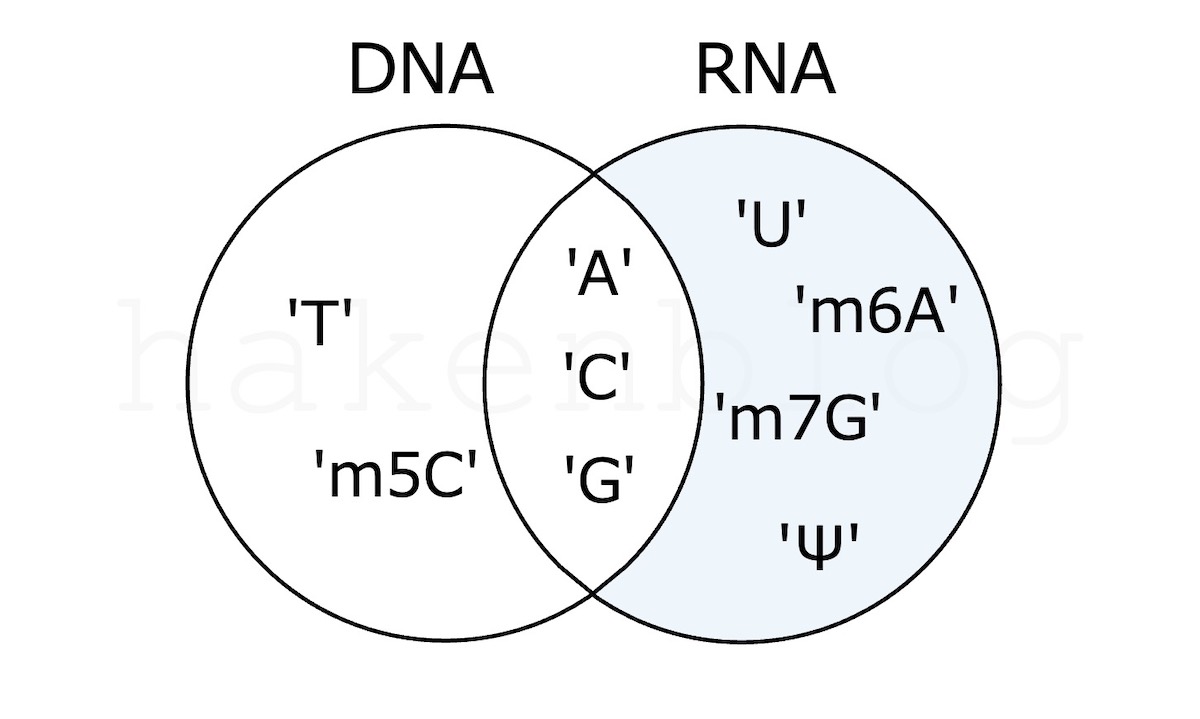
RNA - DNA
RNA.difference(DNA)
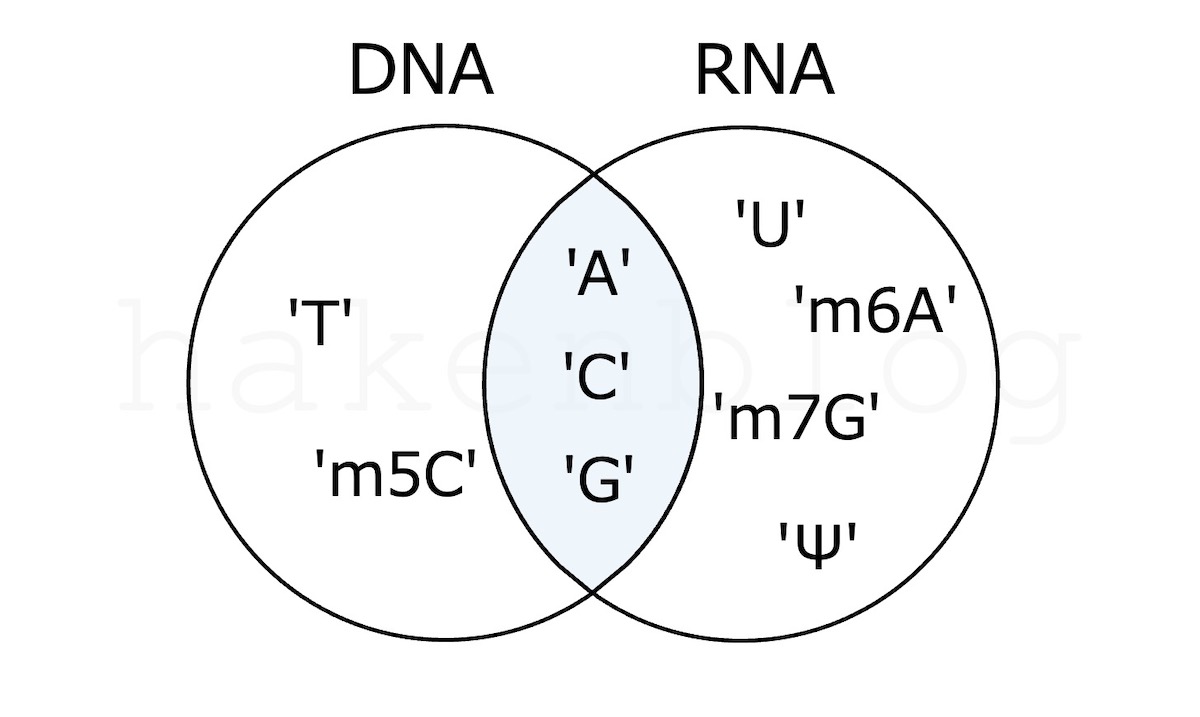
積集合
DNA & RNA
DNA.intersection(RNA)
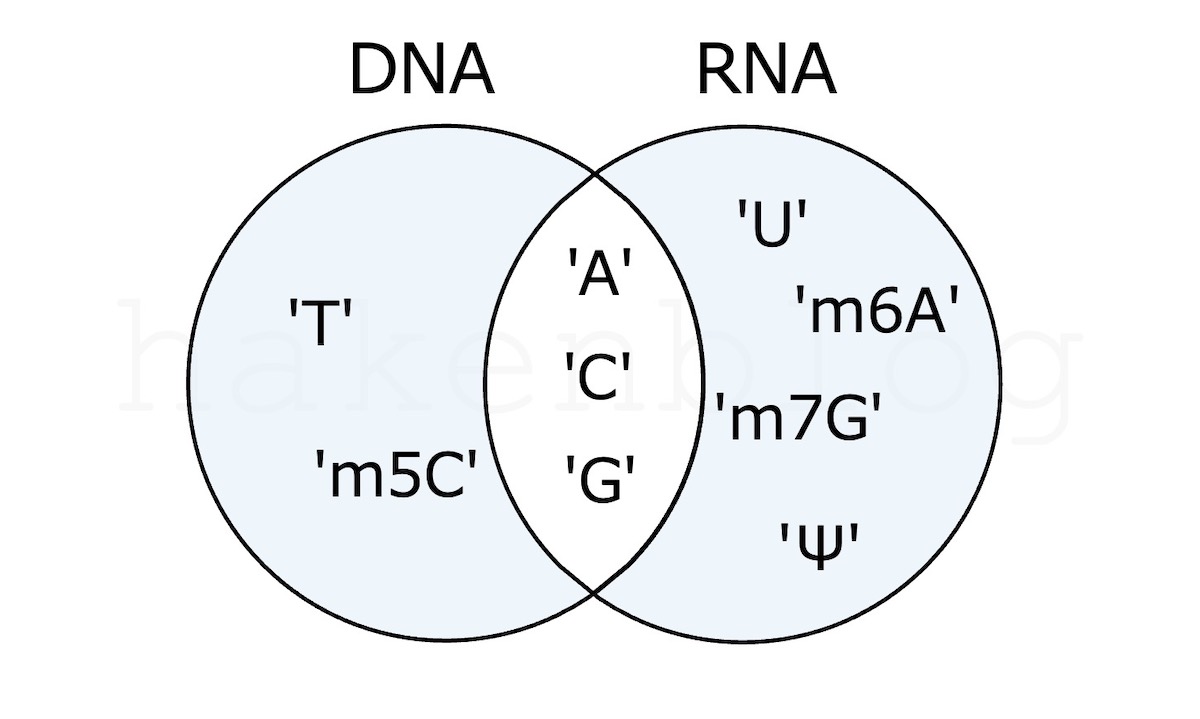
対称差
DNA ^ RNA
DNA.symmetric_difference(RNA)
集合について,基本を学べましたでしょうか?
次は「ブール型と比較演算子・論理演算子」について学びましょう!

最後まで読んでくださり,ありがとうございます☺️